모델링을 하고 난 뒤에 항상 수반되어야 하는 것은 모델의 성능을 평가하는 것이다.
성능 평가를 하기 위해서는 기준이 필요하기 때문에 목적에 따라 다양한 평가지표를 활용하여 성능평가를 진행한다.
이때, 회귀모델과 분류모델의 평가지표가 다르다.
분류모델 평가지표
먼저 분류모델의 평가지표를 알아보도록 하자.
분류모델도 두가지로 나눌 수 있는데, 이진분류모델과 다중분류모델로 나눌 수 있다.
이진분류모델
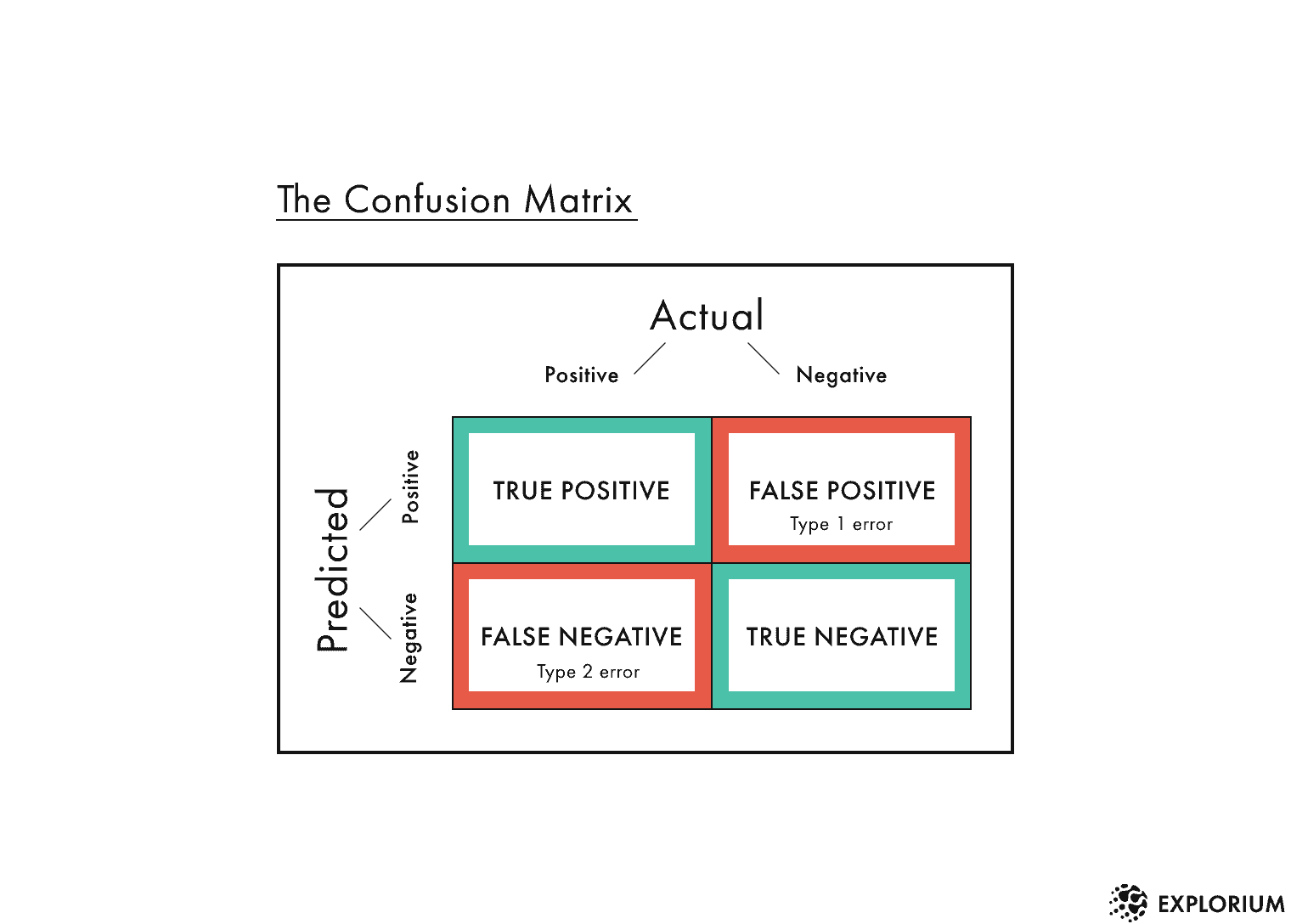
이 중 이진분류모델의 평가지표는 혼동행렬(Confusion Matrix)을 필수적으로 이해해야 한다.

코로나19를 예시로 간단하게 설명하자면,
Actual : 실제 감염여부 / Predicted : 검사결과로 이해하면 된다. 그러면,
- TP : 실제 감염되었고, 검사결과도 양성인 경우
- FP : 실제 감염되지 않았지만, 검사결과가 양성인 경우
- FN : 실제 감염되었지만, 검사결과는 음성인 경우
- TN : 실제 감염되지 않았고, 검사결과도 음성인 경우
위와 같은 4가지 케이스가 나온다.
이때 사용하는 모든 평가지표들은 다음과 같다.
- 정확도 : $$ Accuracy = \frac{TP + TN}{TP + FP + FN + TN} $$
- 전체 데이터에 대해서 정확하게 예측할 확률
- 정밀도 : $$ Precision = \frac{TP}{TP + FP} $$
- 예측결과 양성일 때, 정확하게 예측할 확률
- 재현율(민감도) : $$ Recall(Sensitivity) = \frac{TP}{TP + FN} $$
- 실제 양성일 때, 정확하게 예측할 확률
- 특이도 : $$ Specificity = \frac{TN}{TN + FP} $$
- 실제 음성일 때, 정확하게 예측할 확률
- F1 score : $$ F1 score = \frac{2 * precision * recall}{precision + recall} $$
- 정밀도와 재현율의 조화평균으로 두 값이 모두 높아야지만 F1 score가 증가하고 어느 한 지표라도 성능이 떨어지면 값이 확 떨어짐
- AUC(Area Under the roc Curve) : ROC 그래프의 밑부분 면적
- AUC = 0.5 : Worst Case
- AUC = 1 : Best Case

다중분류모델
다중분류모델의 평가지표는 이진분류의 경우처럼 혼동행렬로 지표를 만들기에는 경우가 너무 다양해서 사용하지 않는 편이다.
그 대신 사용하는 지표로는 지니계수와 엔트로피가 있다.
- Gini Index : $$ Gini=1-\sum_{i=1}^np_{i}^2 $$
- Cross Entropy : $$ Entropy = -\sum_{c=1}^My_{o,c}\log(p_{o,c}) $$
회귀모델 평가지표
회귀모델의 평가지표는 분류모델과는 다르게 예측값과 실제값의 차이를 기준으로 다양한 평가지표를 설정하여 사용한다.
가장 대표적으로는 MSE(Mean Squared Error)가 있으며, 그 외에도 다양한 지표들이 존재한다.
- MSE(Mean Squared Error, L2 norm) : $$ MSE = \frac{1}{n}\sum(Y_i-\hat{Y}_i)^2 $$
- RMSE(Root Mean Squared Error) : $$ RMSE=\sqrt{MSE}=\sqrt{\frac{1}{n}\sum(Y_i-\hat{Y}_i)^2} $$
- RMSLE(Root Mean Squared Log Error) : $$ RMSLE = \sqrt{\frac{1}{n}\sum(log(\frac{\hat{Y}_i + 1}{Y_i + 1}))^2} $$
- MAE(Mean Absolute Error, L1 norm): $$ MAE = \frac{1}{n}\sum\|Y_i-\hat{Y}_i\| $$
- R squared score(결정계수): $$ R^2=1-\frac{SSR}{SST}=1-\frac{\sum(Y_i-\hat{Y}_i)^2}{\sum(Y_i-\bar{Y})^2} $$
- 추정한 선형 모형이 주어진 자료에 적합한 정도를 재는 척도로, 종속변수(y)의 분산 중에서 적합된 모형이 설명가능한 부분의 비율을 의미한다.
분류/회귀 모델을 평가할 때 위 지표들을 적절하게 활용하여 성능을 끌어올리는 일을 무한반복해주는 것이 머신러닝의 가장 핵심 중 하나다.
그럼,
Adios!
반응형
'Data Science > Machin Learning' 카테고리의 다른 글
| [ML] Feature Engineering (0) | 2022.11.09 |
|---|---|
| [ML] (Clustering)K-means Clustering (0) | 2022.11.07 |
| [ML] (Classification) Linear Classification (0) | 2022.10.28 |
| AI, 그게 뭔데? (0) | 2022.09.12 |
| Macbook M1 Tensorflow 설치하기(for jupyter notebook) (0) | 2022.09.12 |